3.1. Mathematical properties of vectors

 

3.1.1. The symmetry transformations

 

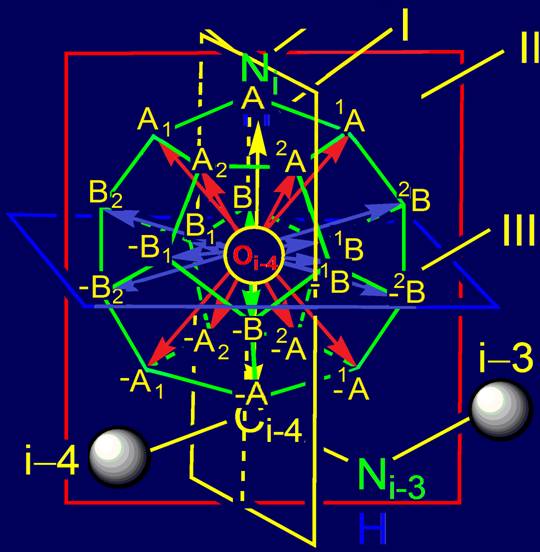
Vector, allocated in the field N_iH…O_i-4=C-bond, as a result of dodecahedron introduction have appeared its radii which are starting from the centre in which O_i-4 atom is placed, and directed to its vertices (fig. 10). Owing to symmetry, the vectors in opposite directions can be considered as well as the diameters of the dodecahedron.

 

The direction of each vector can be characterized by two points: a point from which the radius proceeds - the dodecahedron centre (it is common for all 20 radii), and the point to which the radius is directed, in this case, one of the vertices of the dodecahedron. The positions of these vertices, in principle, can be described using any of the standard methods for describing the coordinates (rectangular, polar, etc.), but for this analysis is not essential. We used for this purpose letter designations introduced in Section 2.3.2.

 

Inside the dodecahedron vectors form four groups connected by mutual transformations of symmetry (Fig. 10).

 

 

Since we have three planes of symmetry, the transition through each plane to a symmetric element can be designated by whatever letter. Following designations have been introduced [1-5]:

– The transition of element in itself is designated by digit 1.

– Transition through a plane I – the letter  a (alpha);

– Transition through a plane I I– letter  b (beta);

– Rotation about an axis lying in the plane III – letter  g (gamma).

All transformation of vectors within each group can be described in the form of table 3.1.

Table 3.1.

The groups of vectors connected by transformations of symmetry

 

The first and the second subgroups of vectors are localized in the plane I. They are yellow and green (Fig. 10), and the vertices to which they are directed are designated A and -A, B and -B. These subgroups include, respectively, two pairs of mutually perpendicular vectors related by the identity transformation (1) of the vector in itself (A -> A, B -> B) and rotation transformation g round axis C₂ concerning a plane III: A -> – A and B -> – B).

 

The third subgroup includes eight vectors, stained in Figure 10 in red and marked with the letters A with the indices. It is connected:

– The identity transformation (1) of the vector in itself (A₁ -> A₁);

– Reflexion transformations a - concerning a plane I (A₁ -> ¹A) and b –concerning a plane II (A₁-> A₂);

– Their combination – ab (A₁ -> ²A);

– Rotation transformation g round axis C₂ concerning a plane III: A₁ -> –A₁;

– A combination of rotation   g with other transformations – ag: A₁ -> –¹A, bg: A₁ -> – A₂, abg: A₁ -> –²A).

 

The fourth subgroup includes eight vectors, stained in Figure 10 in blue and marked with the letter B with indexes. It is connected by the same operations of transformation of symmetry.

So, is available:

– The identity transformation (1): B₁ -> B₁,

– Reflexion a: B₁ -> ¹B, reflexion b: B₁ -> B₂;

– Their combination ab: B₁ -> ²B;

–Rotation g concerning a plane III g: B₁ -> –B₁;

– Various combinations of the rotation: ag: B₁ -> –¹B, bg: B₁ -> –B₂, abg: B₁ -> –²B.

 

All these operations, done for A₁ and B₁, can be made for any of the vectors of these two groups.

 

3.1.2. Vectors as a mathematical group

 

The group-theoretic approach has proved very effective in theoretical physics [16]. We applied it to analyze the properties of MVM vectors. Before making such an analysis, we recall the basic axioms of group theory [16].

 

Group definition: Nonempty set G with the binary operation set on it: G x G --> G is called as group (G) if following axioms are executed in it:

 

1. Associativity: for any a, b and c from G it is true (a · b) · c = a · (b · c);

2. Presence of a neutral element: in G there is an element e such, that for all a from G it is fair e · a = a · e = a;

3. Presence of a inverse element: for any a from G there will be an element a^-1 from G, named the inverse, such, that a · a^-1 = a^-1 · a = e:

Comparison of these axioms to the set of vectors of a dodecahedron allows to say that is group.

 

The associativity of the vectors can be understood in the sense that for any vectors in this group the result of their actions will always be the same, if the sequence of their action remains.

 

The presence of the neutral element presupposes the existence of such a vector, the appearance and effect of which does not change the type of structure.

 

Finally, the existence of inverse element presupposes the existence of a vector, which realization fundamentally changes the character of the structure.

 

Examination of vectors from the position of group-theoretic approach allows us to assume that the vector A, whose action is always directed toward the formation of cyclic 4-unit fragment, is a neutral element, and the vector –A, whose action is always directed to the destruction of 4-unit fragment is the inverse element in this group. A similar group-theoretic approach was used to analyze the properties of the canonical set of amino acid side chains (Section 3.2.).

 

 

To the main page

 

 Address for connection: vector-machine@narod.ru